SISTEMAS DE CONTROLE II
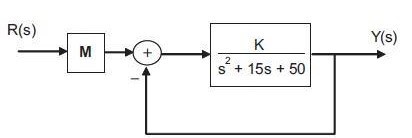
A figura abaixo apresenta o diagrama em blocos de um sistema de controle em malha fechada. Para que no domínio do tempo a saída y(t) siga a entrada de referência r(t), do tipo degrau, com erro de estado estacionário NULO.
Qual a expressão do ganho M?





Qual é a principal consequência da introdução de um atraso de transporte em um sistema de controle?
Aumentar a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, independentemente do valor do atraso.
Aumentar a margem de fase, deixando o sistema mais estável e, possivelmente, estável, dependendo do valor do atraso.
Reduzir a margem de fase, deixando o sistema mais estável e, possivelmente, estável, dependendo do valor do atraso.
Manter a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, independentemente do valor do atraso.
Reduzir a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, dependendo do valor do atraso.
Considere o sistema discreto da Figura abaixo.

Determine a faixa de valores do ganho K de modo que o sistema seja estável em malha fechada.
0 < K < -0,8
0 > K > 0,8
0 > K > -0,8
-0,8 < K < 0,8
0 < K < 0,8
Qual equação abaixo define o método de Tustin?





Considere o sistema de controle apresentado a seguir.
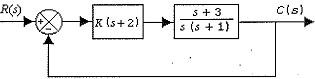
Para a construção do lugar das raízes do sistema acima é preciso calcular os pontos de partida e de chegada. Assinale a opção que apresenta aproximadamente o valor do ganho K nos pontos de partida e de chegada, respectivamente.

Qual é a principal consequência da introdução de um atraso de transporte em um sistema de controle?
Aumentar a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, independentemente do valor do atraso.
Aumentar a margem de fase, deixando o sistema mais estável e, possivelmente, estável, dependendo do valor do atraso.
Reduzir a margem de fase, deixando o sistema mais estável e, possivelmente, estável, dependendo do valor do atraso.
Manter a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, independentemente do valor do atraso.
Reduzir a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, dependendo do valor do atraso.
Considere o sistema discreto da Figura abaixo.

Determine a faixa de valores do ganho K de modo que o sistema seja estável em malha fechada.
0 < K < -0,8
0 > K > 0,8
0 > K > -0,8
-0,8 < K < 0,8
0 < K < 0,8
Qual equação abaixo define o método de Tustin?





Considere o sistema de controle apresentado a seguir.

Para a construção do lugar das raízes do sistema acima é preciso calcular os pontos de partida e de chegada. Assinale a opção que apresenta aproximadamente o valor do ganho K nos pontos de partida e de chegada, respectivamente.
Aumentar a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, independentemente do valor do atraso.
Aumentar a margem de fase, deixando o sistema mais estável e, possivelmente, estável, dependendo do valor do atraso.
Reduzir a margem de fase, deixando o sistema mais estável e, possivelmente, estável, dependendo do valor do atraso.
Manter a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, independentemente do valor do atraso.
Reduzir a margem de fase, deixando o sistema mais oscilatório e, possivelmente, instável, dependendo do valor do atraso.
Considere o sistema discreto da Figura abaixo.

Determine a faixa de valores do ganho K de modo que o sistema seja estável em malha fechada.
0 < K < -0,8
0 > K > 0,8
0 > K > -0,8
-0,8 < K < 0,8
0 < K < 0,8
Qual equação abaixo define o método de Tustin?





Considere o sistema de controle apresentado a seguir.

Para a construção do lugar das raízes do sistema acima é preciso calcular os pontos de partida e de chegada. Assinale a opção que apresenta aproximadamente o valor do ganho K nos pontos de partida e de chegada, respectivamente.

0 < K < -0,8
0 > K > 0,8
0 > K > -0,8
-0,8 < K < 0,8
0 < K < 0,8
Qual equação abaixo define o método de Tustin?





Considere o sistema de controle apresentado a seguir.

Para a construção do lugar das raízes do sistema acima é preciso calcular os pontos de partida e de chegada. Assinale a opção que apresenta aproximadamente o valor do ganho K nos pontos de partida e de chegada, respectivamente.
Considere o sistema de controle apresentado a seguir.

Para a construção do lugar das raízes do sistema acima é preciso calcular os pontos de partida e de chegada. Assinale a opção que apresenta aproximadamente o valor do ganho K nos pontos de partida e de chegada, respectivamente.
